Adatstruktúrák, amiket ismerned kell
Mi köze a családfának, a Neptun-kódoknak vagy egy halom tányérnak a programozáshoz?
Az adatstruktúrák az informatika fontos alapkövei, a programozás alapjait jelentik. Lehetőséget biztosítanak nagy mennyiségű adat kezelésére. A jól működő adatszerkezetek kulcsfontosságúak a hatékony algoritmusok tervezésében, a szoftverfejlesztésben.
Az adatstruktúráknak, vagyis az adatok digitális rendszerezésének számos formája van – a továbbiakban a legalapvetőbb felépítéseket nézzük végig.
#1. Tömb/Array
A tömb a legegyszerűbb és legszélesebb körben használt adatstruktúra, sok más rendszerezésnek is az alapját jelenti. Az olyan fix méretű adatstruktúrát nevezzük tömbnek, amely azonos típusú elemekből áll (számok, értékek), és mindegyiket legalább egy index vagy kulcs azonosítja. A tömb mérete nem módosítható, mivel rögzített méretű elemeket tartalmaz. Ha ilyen műveletet szeretnénk, akkor létre kell hoznunk egy új tömböt a megnövelt mérettel, átmásolni az elemeket, majd hozzáadni az újat.
Leginkább úgy lehet elképzelni, mintha a tömb egy könyv lenne, az elemek pedig az oldalak, amelyeket a számozással lehet azonosítani (ez az indexe). Amikor információt keresünk, akkor az adott oldal indexére hivatkozunk, azaz az oldalszám alapján találjuk meg.
A legegyszerűbb típusa a lineáris, más néven egydimenziós tömb, de léteznek többdimenziós változatok is (tömbök a tömbökön belül).

Forrás: towardsdatascience.com
A tömböket gyakran építőelemként használják más adatstruktúrák felépítéséhez. Emellett különböző rendezési algoritmusokhoz is használható, mint például a beszúrásos rendezés, a gyors rendezés vagy az összevonási rendezés.
#2. Láncolt lista/Linked list
A lista vagy „láncolt lista” struktúrában az adatok lineáris sorrendben vannak elhelyezve és egymáshoz kapcsolva. Sajátossága, hogy nem tudunk véletlenszerűen hozzáférni egy-egy adathoz, azokat csak sorrendben lehet elérni.

Forrás: towardsdatascience.com
A lista első elemét fejnek (head), az utolsó elemet pedig faroknak (tail) nevezzük. A lista elemei a node-ok, azaz csomópontok. Minden csomópont tartalmaz egy hivatkozást is a következő csomópontra (next). Aszerint, hogy hogyan milyen irányba haladhatunk, háromféle listastruktúrát különböztetünk meg:
- Egyszerű összekapcsolt lista: az elemek között csak egy irányba haladhatunk.
- Duplán kapcsolt lista: az elemek között előre és hátra is haladhatunk.
- Körkörösen összekapcsolt lista: az első és utolsó elem össze van kötve egymással.
A láncolt szerkezetnek köszönhetően viszonylag egyszerű az elemek törlése vagy beszúrása a lista bármely pontján, ugyanakkor a keresés, egy véletlenszerűen kiválasztott elem előkerítése a lista hosszával arányos időt igényel.
A csomópontok adatmezői tetszőleges adatot tárolhatnak, így akár hivatkozást is egy másik láncolt listára. Ezzel a trükkel már nem csak lineáris adatszerkezeteket tudunk építeni, hanem tetszőleges elágazó struktúrát, mint például fákat, gráfokat.
#3. Verem/Stack
A stack – magyarul verem – struktúra lényege a LIFO-elv (Last In First Out), azaz hogy az utoljára elhelyezett elemet érjük el legelőször. Az adatokat úgy kell elképzelni, mintha egy tányérhalom lenne, ahol mindig a legfelsőt, vagyis a legutoljára odahelyezettet tudjuk levenni. Lehetőségünk van új elem hozzáadására (push) vagy a legutolsó elem törlésére (pop). Van egy harmadik művelet is, az ún. peek, amikor is visszakapjuk a legfelső elemet anélkül, hogy törölnénk azt.
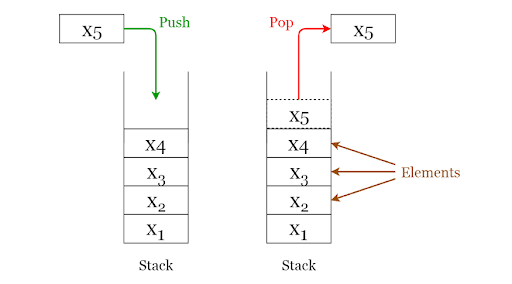
Forrás: towardsdatascience.com
#4. Sor/Queue
A queue, azaz sor a stackhez nagyon hasonló adatszerkezet, azonban a LIFO-elv helyett itt a FIFO érvényesül (First In First Out), vagyis az elsőként berakott elemet érjük el elsőként. A nevéhez hűen legjobban úgy lehet elképzelni, mint mikor sorban állunk például egy épület előtt. Aki elsőként állt be sorba, az jut be elsőként, míg a sor legvégén állók lesznek az utolsók. Ennek mentén tehát ebben a struktúrában új elemet a sor végéhez tudunk hozzáadni, míg törölni a sor elejéről tudunk.
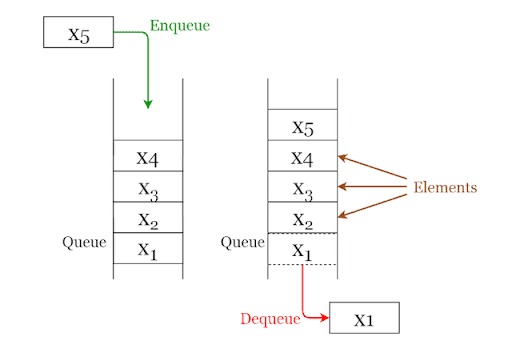
Forrás: towardsdatascience.com
Általában akkor használjuk, ha priorizálni szükséges az adatokat, folyamatokat.
#5. Hash-tábla/Hash table
A hash egy olyan adatszerkezet, ahol minden értékhez kulcsok tartoznak. Ennek köszönhetően a hasonló elemek csoportjában könnyen megtalálható egy adott elem. Hasonlóan működik, mint egy könyvtár, ahol egy adott könyv helyét a megfelelő adatokkal tudjuk meghatározni (ezek a kulcsok). Vagy mikor egy egyetemen a hallgató kap egy azonosítót (pl.: Neptun-kód), ami alapján minden adata könnyen kereshető és elérhető. Ezt a struktúrát gyakran az információk titkosítására is használják.

Forrás: towardsdatascience.com
#6. Fa/Tree
A fastruktúrában az adatok a listákhoz hasonlóan kapcsolódnak egymáshoz, azonban a lineáris elrendezés helyett itt hierarchikusan épülnek egymásra az elemek. Több különböző típusú fát is kifejlesztettek az idők során, hogy megfeleljenek a változó igényeknek. Ilyen például a bináris keresőfa, a piros-fekete fa vagy a kiterjesztett fa. Az adatstruktúrának, csakúgy mint egy igazi fának, gyökerei, ágai és levelei vannak. A felépítés és az elnevezések leginkább a családfákhoz hasonlítanak: a csomópontot, amelynek nincs „őse”, gyökércsomópontnak nevezzük, a többit szülő- és gyerekcsomópontoknak. Emellett léteznek testvércsomópontok, amelyek azonos szülővel rendelkeznek. A fa leveleit azok a gyerekcsomópontok alkotják, amelyeknek már nincsen leszármazottja.

Forrás: towardsdatascience.com
A fastruktúrákat használják a fejlesztők például videójátékok esetén, mert segítségükkel egyszerűen felosztható a tér, gyorsan megtalálhatók tárgyak vagy irányok. Egy négy csomóponttal rendelkező fával (quadtree) például létrehozható egy, a négy égtáj szerinti térkép a játékon belüli tájékozódáshoz.
#7. Halom/Heap
A heap a bináris fastruktúra egy speciális esete, amikor a szülőcsomópontokat összehasonlítjuk a gyerekeikkel, majd az értékeket ennek megfelelően rendezzük. Ezek alapján kétféle halom létezik:
- Min. heap, ahol a szülő kulcs értéke egyenlő vagy kisebb, mint a gyerekek kulcsai.
- Max. heap, ahol a szülő kulcs értéke nagyobb, mint a gyerekek kulcsa.
A halmokat széles körben használják egy tömb legnagyobb és legkisebb értékének megtalálására, valamint algoritmusokban prioritási sorok létrehozására.

Forrás: towardsdatascience.com
#8. Mátrix
Mátrixnak nevezzük azokat a kétdimenziós struktúrákat, melyek sorokból és oszlopokból állnak. Gyakorlatilag egy téglalap alakú tömbről van szó, amelynek méretét a sorok és oszlopok száma határozza meg. A matematikában a lineáris algebrai egyenletek vagy differenciálegyenletek rövid leírására, illetve a valószínűségszámításban használják. A mindennapokban is találkozhatunk mátrixstruktúrával, ilyen például az oldalak rangsorolása a Google-keresőben (a PageRank algoritmus segítségével). A számítógépes grafikában szintén a mátrix struktúra segítségével tudunk 3D-
modellekkel dolgozni, azokat kétdimenziós képernyőre vetíteni.
A fentiekben felsorolt alapvető adatszerkezeteken túl számos bonyolultabb struktúra is létezik. Az alapok birtokában azonban akár saját egyedi struktúrák létrehozására is lehetőség nyílik.





